Doğa Altın Oranı Seviyor
Doğa Altın Oranı Seviyor


Sarmal biçimli kabuğunun içinde yaşayan bir kafadan bacaklı olan notilus, iki üstte Büyük Okyanus’ta yüzerken görülüyor. Onun altında da bir notilus kabuğu kıyıya vurmuş.


Altın Oran Nedir?
Altın Oran Nedir?
Altın oran, bir bütünün parçaları arasındaki ilginç bir oran bağıntısıdır. Matematikçiler bunu şöyle söyler: İki sayının toplamını büyük sayıya böldüğünüzde çıkan oran ile büyük sayının küçük sayıya oranı birbirine eşitse, buna altın oran denir.
Eğer kafanız karıştıysa aşağıdaki şekle bakabilirsiniz. Bir kenarı a olan bir kare ile ona bitişik ve kısa kenarı b olan bir dikdörtgen düşünelim. a+b toplamının a’ya bölümü, a’nın b’ye bölümüne eşitse, a ve b arasındaki orana altın oran denir. Hem kenarları a ve b olan pembe dikdörtgene hem de kenarları a+b ve a olan dıştaki dikdörtgene de altın dikdörtgen denir.
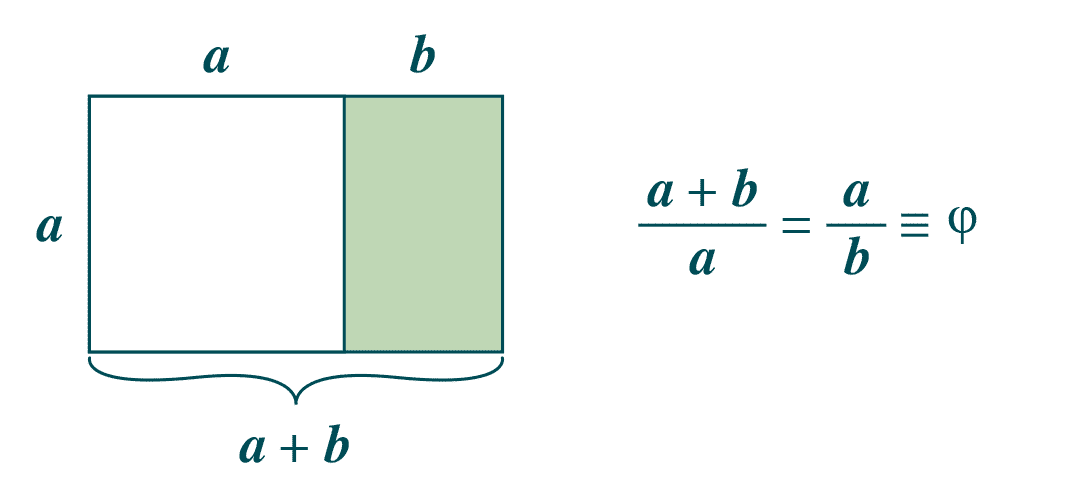

Eğer elinize bir kalem alıp yukarıdaki yeşil dikdörtgenin içine bir kare çizerseniz, yeni oluşacak küçük dikdörtgen de altın orana sahip olur. Bu işlemi tersten yaparsanız, yani dıştaki dikdörtgenin altına ya da üstüne bir kare çizerseniz, ortaya çıkacak büyük dikdörtgenin kenarları da altın oranı verir. İç içe çizilen bu dikdörtgenlerin bir köşesinden diğerine yaylar çizerek onları birleştirince de... Ta taaam! Ortaya tanıdık bir sarmal çıkar. Çünkü bazı canlılarda gördüğümüz sarmal biçimleri altın oranla elde edilen bu sarmala benzer.
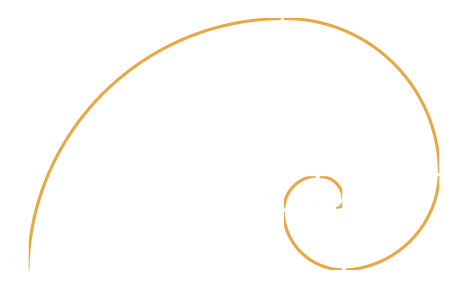
Fibonacci’nin Gizemli Sayıları
Fibonacci’nin Gizemli Sayıları
Elde edilen bu oran rakamlara döküldüğünde 1,618… şeklinde uzayıp giden bir sayı karşımıza çıkar. Ünlü İtalyan matematikçi Fibonacci, 1202’de belli bir kuralı olan ve sonraları kendi adıyla anılan bir sayı dizisi ortaya atmıştı: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, … Bu dizideki kural, peş peşe gelen iki sayının toplamının bir sonraki sayıyı vermesidir. Ve sayılar büyüdükçe ardaşık iki Fibonacci sayısı arasındaki oran tanıdık bir sayıya giderek yaklaşır: 1,618.

Bir ayçiçeğine yakından baktığınızda çekirdeklerin merkezden dışa doğru sarmallar çizdiğini görebilirsiniz.

Sukulent bitkisinin yapraklarının yerleşimi de sarmal biçimindedir.
Doğa Neden Altın Oranı Sever?
Doğa Neden Altın Oranı Sever?
“Peki, doğa neden altın oranı sever?” dediğinizi duyar gibiyiz. Aslında bunun akla çok yatkın bir nedeni vardır. Bir ayçiçeğinin yeni çıkacak çekirdeklerine ya da bir sukulentin yeni açacak yapraklarına en uygun yer için bulduğu çözüm, bunları bir sarmal şeklinde yerleştirmektir. Yeni bir çekirdek ya da yaprak öncekilerin yanına düz bir çizgi gibi dizilmez, en çok güneş ışığı alabileceği yeri arar. İçteki sıranın dışına çıktıktan sonra biraz dönerse, bu iş olur! Sonraki çekirdek ve yapraklar da aynı “altın” kuralı izleyince işte, bu sarmallar ortaya çıkar. Böylece hem göze hoş görünen hem de bitkinin tüm yüzeyini sıkı bir şekilde dolduran bir biçim belirir.

Bazı kabuklu deniz hayvanlarının kabukları da sarmal çizerek gelişir.
İşin ilginç yanı, ayçiçeğinde ya da çam kozalağında görülen bu sarmal kolların toplam sayısı Fibonacci sayılarından birini (5, 8, 13, 21 gibi) verir. Yandaki şekilde bir çam kozalağı üzerindeki sarmallardan biri işaretlenmiş durumda. Diğerlerini de siz sayıp çıkan toplama şaşırmak ister misiniz?

Herhangi bir sarmal biçimi içermeyen diğer canlılardaysa başka şaşırtıcı şeyler görülür. Örneğin ağaçların gövdelerinden çıkan dalların sayıları aşağıdan yukarıya doğru Fibonacci serisindeki sayılar şeklinde artar. Alttaki iki seviyedeki dalların toplamı, bunların üstündeki dal sayısını verir. Aynı şeyi yapraklarda da gözleyebilirsiniz. Böylece, gelişmek için sınırları belli bir alanı değerlendirmesi gereken ağaçların dalları ve yaprakları en çok ışık alacak şekilde yerleşmiş olur.
Siz de doğada altın oranın izini sürmek ister misiniz? Çam kozalaklarında, salyangozlarda, keçi ya da koç boynuzlarında gördüğünüz sarmallara daha dikkatli bakmaya ne dersiniz? Bir ağaçtaki dalları ya da bir papatyanın yapraklarını sayıp şaşırmak ister misiniz? Doğanın altın oranı çok sevdiğini göreceksiniz…




